jussilindgren.fi

Tekijä: admin

  • Weylin geometria ja sähkömagnetismin kiehtova maailma

    Weylin geometria ja sähkömagnetismin kiehtova maailma

    Albertin viimeistelemätön sinfonia

    Albert Einstein käytti elämästään viimeiset 30 vuotta yritykseen yhdistää sähkömagnetismi ja gravitaatio, luonnon kaksi perusvoimaa. Hän ei onnistunut tavoitteessaan. Muita ongelman kanssa painiskelleita tutkijoita olivat mm. saksalainen matemaatikko Hermann Weyl, puolalainen matemaatikko Theodor Kaluza sekä ruotsalainen fyysikko Oskar Klein. Myös kvanttimekaniikan isä Erwin Schrödinger yritti yhdistää sähkömagnetismin ja painovoiman. Säieteoria on teoreettisen fysiikan viimeisin yritys yhdistää perusvoimia, mutta siinä ulottuvuuksia on 11. Eli teoriaa on vaikeaa edes periaatteessa falsifioida. Sir Roger Penrose (Nobel 2020) pitää säieteoriaa vääränä. Nyt on siis tarve ottaa uusia näkökulmia fysiikan perusteorioihin.

    Yleinen suhteellisuusteoria

    Kuva: Andreas Praefcke

    Einstein muotoili yleisen suhteellisuusteorian vuonna 1915, ja esitteli sen ensi kertaa Preussin tiedeakatemiassa. Tiedeakatemia on muuten sama, jonka perusti Leibniz, ja jota muun muassa Maupertuis johti myöhemmin. Akatemia on Berliinissä, Unter den Lindenin lehmusten katveessa. Kaunis talo, ja muistuttaa meitä siitä, mitä hienoa Euroopassa joskus oli.

    Yleisessä suhteellisuusteoriassa painovoimaa ei oikeastaan ole, vaan kappaleet kulkevat lyhimpiä maailmanviivoja neliulotteisessa aika-avaruudessa. Aika-avaruus on kaareutunut, ja jännite-energiatensori on aika-avaruuden kaarevuuden lähde. Teorian ennustamat tulokset on vahvistettu monta kertaa. Teoriassa massa kertoo aika-avaruudelle kuinka kaareutua, ja aika-avaruus kertoo kappaleille, kuinka liikkua. Teoria on kaunis, ja siinä on määrättyä teologista estetiikkaa. Kvanttimekaniikka on rumaa, eikä kukaan oikein ymmärrä sen monia tulkintoja. Kvanttimekaniikan yhtälöt ovat kuitenkin toimivia, ja ne on testattu monta kertaa. Yleisessä suhteellisuusteoriassa Einsteinin kenttäyhtälöt voidaan johtaa minimoimalla tiettyä kokonaiskaarevuusfunktionaalia. Kenttäyhtälöt ovat epälineaarisia tensoriyhtälöitä, eli käytännössä vaikeita ratkoa. Yhtälöt ennustavat mm. mustan aukon, kun jotkut ratkaisut yhtälöissä pitävät sisällä singulariteetteja (jakaja menee nollaan). Yhtälöt ennustavat myös gravitaatioaaltoja, jotka ovat viimein myös löytyneet havainnoissa, aivan viime vuosina. Teoria siis on hyvä, koska se toimii, ennustaa, on yksinkertainen ja falsifioitavissa.

    Yllä Einsteinin kenttäyhtälöt. Jännite-energiatensori on yhtälön oikealla puolella. Einstein ei ollut teoriaan täysin tyytyväinen, koska jännite-energiatensori on vähän ulkopuolinen asia, eikä teoria ole jossain mielessä suljettu ja täydellinen. Vasemmalla puolella on Einsteinin tensori lisättynä kosmologisella vakiolla Lambda. Einsteinin tensori on eräänlainen sopivan symmetrinen kaarevuustensori, joka on myös lähteetön tai divergenssivapaa.

    Weylin geometria

    Yleinen suhteellisuusteoria perustuu pseudo-riemannilaiseen differentiaaligeometriaan. Sen keskeinen ominaisuus on se, että metrisen tensorin kovariantti derivaatta on aina nolla. Weylin geometria on laajennos ja yleistys, jossa metrisen tensorin kovariantti derivaatta voi olla nollasta poikkeava. Suomeksi se tarkoittaa sitä, että pituus käsitteenä on aidosti lokaali eli suhteellinen asia. Muistamme suhteellisuusteoriasta pituuksien muuttumisen nopeuden funktiona jne. Eli Weylin geometria on oikeasti se ”oikea” geometria, ja juuri oikea suhteellisuusteoriaan. Ja rakas ystäväni, kaikki on suhteellista! Hermann Weyl oli lukenut paljon filosofiaa, mm. Kantin käsityksiä ajasta ja avaruudesta, Fichteä olemisesta ja eksistenssistä. Myös Husserlin fenomenologiaan hän tykästyi. Kuriositeettina: myös logiikkanero Kurt Gödel piti Husserlin fenomenologiasta. Weylin geometria poikkeaa siis jonkin verran tavallisesta pseudo-Riemannin monistoista (monisto on diffisgeometrian termi, ja se tarkoittaa sitä kokonaisuutta, missä metrinen tensori määrittää sen, kuinka vektoreiden sisätulo lasketaan.). Monisto tavallaan leivotaan kasaan lokaalisesti alueista, jossa voidaan piirrellä tangenttivektoreita. Pseudo-riemannilainen geometria on tavallaan kohtisuorassa Weylin geometrian kanssa, koska edellisessä vektoreiden suunnat ovat suhteellisia, tai lokaaleja, mutta suuruudet ovat invariantteja. Weylin geometria sallii myös vektoreiden pituuksien olevan suhteellisia tai lokaaleja ilmiöitä.

    Sähkömagnetismi

    Maxwell kuvasi sähködynamiikan 20 yhtälöllä. Nykyisin sähköinsinöörit oppivat ne vektorianalyysin muodossa näin:

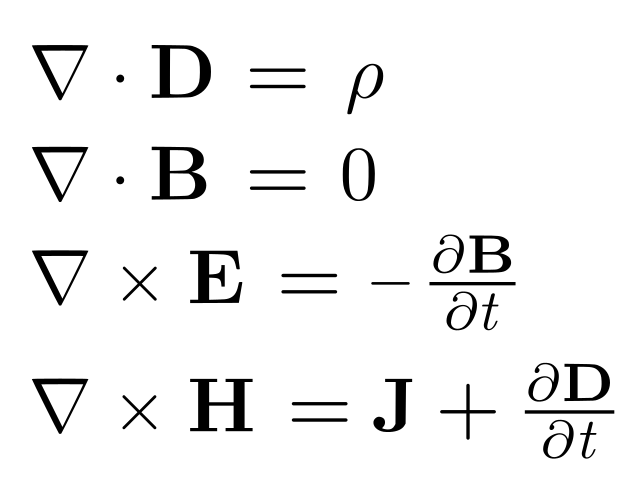
    Ensimmäinen yhtälö kertoo meille sen, että varaus luo ympärilleen sähkökentän. Eli varaustiheys on verrannollinen sähkövuon tiheyden divergenssiin. Toinen yhtälö kertoo meille sen, että magneettivuon tiheyttä kuvaava vektorikenttä on lähteetön, magneettisia monopoleja ei ole. Kolmas yhtälö on Faradayn induktiolaki: muuttuva magneettikenttä on sähkökentän pyörrekentän lähde. Tavattoman tärkeä laki Fortumille ja Teollisuuden voimalle. Hienommin ilmaistuna induktiolaki on yhtäpitävä kaarevuustensorin eräiden symmetriaominaisuuksien kanssa.

    Neljäs laki on Amperen-Maxwellin laki, se liittää ensijaisesti magneettivuon pyörrekentään lähteeksi sähkövirran ja siirrosvirran. On tärkeää huomata, että yhtälöissä on määrätty vinosymmetrinen rakenne. Se liittyy myös analyyttisten funktioiden teoriaan ja harmonisten funktioiden teoriaan. Yhtälöt ovat niin kauniit, että ne saavat uskomaan korkeampaan älyyn ja luomakunnan harmoniaan.

    Tulkoon valkeus!

    Ottamalla roottorin kahdesta jälkimmäisestä yhtälöstä, päästään pienellä vaivalla algebraa nopeasti aaltoyhtälöihin ilman lähteitä. Näin havaitsemme: valo on sähkömagneettisen kentän värähtelyä, jossa magneettikentällä ja sähkökentällä on kohtisuorat värähtelytasot! Polarisaatio on mallin vapausaste.

    Klassinen sähködynamiikka on täydellinen, kun muistamme vielä Lorentzin voimalain: varaukseen vaikuttaa voima, joka on verrannollinen sähkökenttään ja varauksen nopeuden ja magneettikentän ristituloon. Tämä on syy sille, miksi plasma pysyy kasassa Tokamak-fuusioreaktorissa.

    Heittääkö Jumala noppaa?

    Einstein oli sitä mieltä, että ei. Toisaalta kvanttimekaniikka toimii, ja Schrödingerin yhtälö kuvaa hyvin atomin rakenteen. Ominaisarvot ovat energiatasoja, tämä tulee Fourier-sarjojen ominaisuuksista. Olen väitöskirjassani johtanut keskeiset kvanttimekaniikan osittaisdifferentiaaliyhtälöt eräänlaisena likiarvona stokastisen optimisäätötehtävän arvofunktiolle. Teknisesti kaikki keskeiset kvanttipuolen yhtälöt tulevat Hamilton-Jacobi-Bellman yhtälöstä, kun linearisoidaan yhtälöt, ja tarkastellaan arvofunktiota riittävän läheltä, Planckin etäisyyksiltä. Koska painovoima ja kvanttimekaniikka eivät sovi yhteen, on minusta kvanttimekaniikan väistyttävä. Jokin syvempi teoria tarvitaan. Uskon, kuten Nikola Tesla, että ratkaisu on sähkömagnetismissa ja suhteellisuusteoriassa. Einstein oli lopulta voittaja. Hän kuoli 1955 Princetonissa, vielä kuolinvuoteellaan hän yritti yhdistää sähkömagnetismia ja yleistä suhteellisuusteoriaansa.

    Yllä mielenkiintoinen video tämän kirjoituksen teemoista. Alla myös ihan katsomisen arvoinen video.

  • Koulurauha on jokaisen lapsen perusoikeus

    Koulurauha on jokaisen lapsen perusoikeus

    Helsinkiläisten koulujen levottomuus on lisääntynyt, ja alueiden erot korostuvat. Esimerkiksi viime vuoden loppupuolella luimme Pukinmäenkaaren peruskoulun ongelmista. Opettajien mukaan: ’väkivallasta, varastelusta ja nimittelystä on tullut arkipäivää kouluissa’. Maan hallitus on onneksemme suunnannut resursseja koulupoliisitoimintaan miljoonilla euroilla.

    Rauhallinen ja turvallinen kouluympäristö on ensisijaisen tärkeä lasten tulevaisuuden ja aikuisuuden kannalta. Peruskoulu antaa avaimet ja perusedellytykset jatko-opintoihin ja aikuisuuteen.
    Nykypäivän maailmassa vain osaajat työllistyvät, siksi lukeminen, laskutaito ja kirjoitustaito ovat välttämättömiä. PISA-tulosten heikkeneminen kertoo kuitenkin huonosta trendistä.

    Koulurauhattomuuden lisäksi osansa heikkoon kehitykseen on myös asenteilla ja toimintatavoilla. Lapsia ei saa päästää luokalta, elleivät oppimistavoitteet ole täyttyneet. Riman laskeminen on
    karhunpalvelus lasten tulevaisuuden kannalta. Asennemuutos ei tarvitse aina uutta rahoitusta. Muutos asenteissa riittää.
    Kännykkäkieltoa koskeva uusi lainsäädäntö on erinomainen uudistus. Koululuokan täytyy olla turvallinen tila oppia. Ei voi olla niin, että pieni vähemmistö terrorisoi koko luokan oppimistuloksia. Perusopetuslaissa on riittävät säännökset ja toimivallat rehtoreille ja opettajille poistaa häiriköt luokasta. Toimivaltuuksia on uskallettava käyttää. Poliisin virka-apu on viimesijainen keino. Lapsiemme perusoikeutena tulee olla turvallinen kouluympäristö sekä koulurauha.

    Kiusaamiseen ja väkivaltaan tulee puuttua viiveettä ja lujasti.
    Lasten levottomuus ja häiriköinti kouluissa kumpuaa varmaankin osin rikkoutuneista kotioloista. Kasvatusvastuu kuuluu kuitenkin edelleen pääosin perheelle, ja mikään opettaja ei voi korvata
    lapselle turvallista kotia, rakastavia äitejä ja isiä. Rajat ovat rakkautta. Suomen kansantaloudenkin kannalta on välttämätöntä, että tulevaisuuden Suomessa on rauhallisessa kasvuympäristössä kasvaneita tulevia putkimiehiä, sairaanhoitajia ja insinöörejä.

    Pitäisi ehkä myöntää itsellemme, että menneestä maailmasta voisimme oppiakin jotakin. Jokin on muuttunut huonoon suuntaan vuosien saatossa, koska lapsiemme perusosaaminen on romahtanut. Yläluokilta voi siirtyä nuoria ihmistaimia ammattikouluihin ja lukioihin todella heikolla
    osaamisella. Valitettavasti myös eriytyminen jatkuu asuinalueittain. Jos emme tartu tiukasti näihin ongelmiin, yhteiskunnan luottamus rapautuu, asuinalueet jakautuvat hyviin ja huonoihin. Turvattomuus, rikollisuus, katuväkivalta ja aikuisuuden ongelmat ovat heijastumia koulumenestyksestä tai sen puutteesta. Siksi koulurauha on turvattava kaikissa Helsingin kouluissa.

    Oletan, että toimia tarvitaan etenkin Opetushallituksessa. Idealismi, woketus, naiivismi ja muu hörhöily on korvattava realismilla ja älykkäällä tietoisuudella tosiasioista. Suomalainen yhteiskunta on siirtymässä vaiheeseen, jossa heikot johtajat (1995-2023) ovat olleet omiaan luomaan vaikeita aikoja. Opettajille tulee palauttaa auktoriteetti. Pääkaupunkiseudulla on nähtävissä selvästi kehitys, jossa koulut täyttyvät riehuvista maahanmuuttajaluokista. Kuka tavallinen suomalaisperhe haluaa lapsensa tuollaiseen helvettiin. Idealismi, sosialismi, feminismi ja muut kulttuurivallankumoukselliset hulluudet tuhoavat yhteiskuntamme. Aikaa ei ole hukattavaksi.

    Äänestä perussuomalaisia. Pian on myöhäistä.

  • Miten SOTE:a tulisi kehittää?

    Miten SOTE:a tulisi kehittää?

    Suomalainen terveydenhoidon malli on kehittynyt kunnanlääkärijärjestelmästä terveyskeskusmallin kautta hyvinvointialueisiin vuosikymmenten saatossa. Terveyskeskusmalli syntyi Ahti Karjalaisen II hallituksen aikana, vuonna 1972. Mallia oli haettu muun muassa kansandemokratiasta, eli sosialistisesta DDR:stä. Hyvinvointialueet rahoitusmalleineen syntyivät punamullan voimin vuonna 2021. Alueet aloittivat tammikuussa 2023. Nykyinen tasavallan hallitus lisäsi alueille rahoitusta kuluvalle vuodelle lisää noin 2,2 miljardia euroa. Alueiden talous on tasapainottumassa, mutta kehitysvaraa vielä löytyy. Hyvinvointialueiden rahoituslaskelmiin voit perehtyä täällä:

    https://vm.fi/rahoituslaskelmat

    Valtiovarainministeri Riikka Purran hiljattain ilmestynyt kirjoitus Kansantaloudellisessa aikakauslehdessä löytyy täältä:

    https://journal.fi/kak/article/view/159750

    Suomalainen sosiaalihuollon ja perusterveydenhoidon järjestelmä ei ole mielestäni mitenkään kriisissä. Erikoissairaanhoito toimii melkoisen hyvin. Hoitoon pääsee itse asiassa ihan kohtuullisen hyvin.

    https://thl.fi/tilastot-ja-data/tilastot-aiheittain/terveyspalvelut/hoitoonpaasy-perusterveydenhuollossa

    https://thl.fi/tilastot-ja-data/tilastot-aiheittain/terveyspalvelut/hoitoonpaasy-erikoissairaanhoidossa

    Isoja ongelmia liittyy siihen, että vanhukset joutuvat jonottamaan hoitoon terveyskeskuksissa, kun taas työterveyshuollossa tuntuu olevan ylitarjontaa palveluissa. Jotenkin meidän täytyisi saada työterveyden kapasiteettia suunnattua vanhusväestölle. Valtion ja alueiden pitäisi joko ostaa tätä volyymia, tai sitten lääkäreitä pitäisi saada lisää ja lisää töihin hyvinvointialueille. Kielitaidottomista tuontihoitajista ei ole kestäväksi ratkaisuksi.

    Sote ei ole sen kalliimpi kuin monessa verrokkimaassa. Suomi käyttää soteen tänä vuonna suoraan reilut 26 miljardia euroa, mikä vastaa noin vajaata 10 prosenttia bruttokansantuotteesta.

    https://stm.fi/-/eurooppalainen-vertailu-suomalaisten-terveys-verrattain-hyva-pitkat-jonotusajat-vaikeuttavat-terveyspalvelujen-saatavuutta

    Suomalaista mallia kannattaisi kuitenkin uudistaa. Alla on ajatelmiani siitä, miten suomalaista mallia voisi kehittää.

    Meidän tulisi luoda Suomeen uusi omalääkärimalli, joka voisi hyödyntää vaikkapa Hollannin terveydenhoitojärjestelmän vahvuuksia, kuten vahvaa perusterveydenhuoltoa, perhelääkärien keskeistä roolia ja ehkä jopa suurempaa vakuutuspohjaista rahoitusta. Toisaalta uuden omalääkärimallin tulisi mukautua Suomen olemassa olevaan infrastruktuuriin, väestörakenteeseen ja hyvinvointialueiden järjestelmään.

    Jokaiselle suomalaiselle osoitettaisiin oma perhelääkäri (yleislääkäri), joka toimisi ensisijaisena kontaktipisteenä terveydenhuollossa. Perhelääkäri vastaisi potilaan kokonaishoidosta, ennaltaehkäisystä ja hoitopolun koordinoinnista. Potilaat listautuisivat perhelääkärille, ja kullekin lääkärille määriteltäisiin sopiva vastuuväestö. Perhelääkärit voisivat toimia joko julkisella sektorilla (hyvinvointialueilla) tai yksityisinä ammatinharjoittajina/yrityksinä, mutta heillä olisi sopimus hyvinvointialueen kanssa, joka takaa palveluiden saatavuuden kaikille.

    Potilaat varaisivat ajan suoraan omalta perhelääkäriltään, ja vastaanotolle pääsisi 1–3 päivän kuluessa kiireettömissä tapauksissa. Kiireellisissä tapauksissa hoito järjestetään saman päivän aikana. Perhelääkäri toimisi tiimissä, johon kuuluisi esimerkiksi sairaanhoitaja, fysioterapeutti ja sosiaalityöntekijä. Tämä moniammatillinen tiimi tukisi potilaan kokonaisvaltaista hoitoa, ja vähentäisi lääkärin työtaakkaa.

    Perhelääkäri toimisi portinvartijana: erikoissairaanhoitoon pääsisi vain hänen lähetteellään, paitsi akuuteissa päivystystapauksissa. Tämä vähentäisi turhia erikoissairaanhoidon käyntejä, ja tehostaisi resurssien käyttöä. Perhelääkärit voisivat tehdä kotikäyntejä erityisesti iäkkäille tai liikuntarajoitteisille potilaille, mikä parantaisi hoidon saatavuutta haja-asutusalueilla.

    Lääkäreiden koulutusta voitaisiin myös lisätä maltillisesti, samoin lääkärivirkoja. Lääketieteellisiä tiedekuntia voitaisiin skaalata ylös palkkaamalla opetushenkilöstöä ja tutkijoita ulkomailta lisää.

    Terveyden edistäminen ja liikuntapaikkojen lisääminen pitäisi näkyä vahvemmin kaupunkimme strategiassa myös. Uimahallit ja punttisalit tarjoavat esimerkiksi erinomaisen tavan pitää lääkäri loitolla, etenkin pimeänä ja kylmänä talvikautena.

    Miltä kuulostaa? Jos sinusta tässä pohdinnassa on järkeä, voit äänestää minua kuntavaaleissa Helsingissä numerolla 399.

  • Tarvitsemme yhteiskuntasopimuksen valtion ydintehtävien turvaamiseksi

    Tarvitsemme yhteiskuntasopimuksen valtion ydintehtävien turvaamiseksi

    Englantilainen filosofi Thomas Hobbes (1588-1679) kirjoitti aikanaan valtion syntymisestä anarkian tilalle. Valtio syntyi turvaamaan alueellaan kansalaistensa oikeudet elämään ja omaisuuteen. Yhteisten pelisääntöjen noudattaminen on tärkeää, oli kyse sitten metsästysseurasta tai kokonaisesta yhteiskunnasta. Pakottavan lainsäädännön ohella kulttuurinen ja sosiaalinen koheesio on välttämätöntä. Yhteisten arvojen jakamisesta kaikki lähtee. Suomalainen yhteiskunta on perustunut luottamukseen ja sosiaaliseen koheesioon. Jopa sosialidemokratia toimi 1980-luvun Suomessa, kun vapaamatkustusta oli vähemmän. Sodan nähneet miehet ja naiset eivät valittaneet turhasta jälleenrakennuksen vuosikymmeninä. Junalastit liikkuivat itään ja sotakorvaukset maksettiin. Patruunat pitivät huolen omistaan. Asuin 1990-luvun alussa Kaavilla, Luikonlahden kaivoksen liepeillä. Myllykoski oy oli aloittanut kuparin louhinnan alueella 1960-luvulla, ja yhtiö rakennutti työntekijöille asunnot keskelle metsää, sorvaajasta insinööriin. Yhtiö rakennutti asukkaille mm. rantasaunat, tenniskentät ja punttisalin. Tuollainen markkinatalous on hyvää markkinataloutta. Björnbergit taisivat asua siellä vielä 1990-luvun alussa myös. Vuosikymmeniä myöhemmin muistelen tuota lapsuuden Suomea lämmöllä. Luottamuksen, sosiaalisen koheesion ja yhteistyön Suomea. Se aika ei palaa enää. Monikulttuurisuuden auvon myytti murenee, kun näemme miten kansainvaelluskatastrofi etenee eurooppalaisissa maissa. Sosiaalisen koheesion mureneminen rapauttaa lopulta veronmaksumoraalia. Kovat ajat toisaalta saavat meidät ryhdistäytymään, vätystelyn on aika loppua. Haasteet ovat valtavat.

    Geopoliittiset mannerlaatat liikkuvat nyt nopeasti. NATO:n yhteinen sopimus puolustusmäärärahatavoitteen kasvattamisesta saataneen Haagin huippukokouksesta juhannuksen korvalla. Eurooppa-neuvosto, eli EU:n jäsenmaiden päämiehistä koostuva unionin toimielin, linjaa EU:n puolustusrahoituksesta samoin, viimeistään kesäkuussa. Suomessa valtion alijäämä on yli 12 miljardia euroa vuodessa ja velkaa on kohta jo 200 miljardia euroa. Armeija marssii vatsallaan, maavoimien kalustoa on uusittava, asejärjestelmiä on kehitettävä. Naton pääsihteerin julkisten puheiden perusteella puhutaan jopa 3,5 miljardin euron pysyvistä lisäyksistä valtion kehysmäärärahoihin. Olivat puolustusmenot kehyksessä tai ei, ne lisäävät valtiontalouden alijäämää ja ulkomaille velkaa, jollei korvaavia säästöjä haeta muualta. Sote-menojen kasvu jatkuu, koska väestö ikääntyy. Kokonaisveroasteemme on niin korkea, että verotuksesta ei ole pelastajaksi – lisäverot tässä tilanteessa tappaisivat kasvua liiaksi. Suomessa on 350 000 työtöntä, kun kaikki tempputyöllistetyt lasketaan mukaan. 1970-luvulla oltaisiin kasaamassa jo hätätilahallitusta. Ehkä puolustusobligaatiot kaiken kansan sijoituskohteena voisivat sen sijaan auttaa.

    Seuraava hallitus joutunee sopeuttamaan julkista taloutta noin 10 miljardin euron edestä seuraavan vaalikauden aikana. Tällainen urakka jo tehtyjen säästöjen päälle on valtaisa. Siksi tarvitaan laaja-alaista keskustelua siitä, mitkä ovat valtion ydintehtävät. Puolueiden tulee kertoa jo vaalien alla 2027, mistä ne ovat valmiita tekemään uusia säästöpäätöksiä. Näin kansalaiset voivat tehdä aitoja arvovalintoja ehdokkaiden ja puolueiden välillä. Sotilaallinen maanpuolustus ja sisäinen turvallisuus ovat suojassa leikkauksilta. Näin kuuluu ollakin. Soten leikkauksien osalta rahoituslakia olisi katsottava uudestaan. Rahoitus kasvaa liian nopeasti valtion taloudelliseen kantokykyyn nähden.

    Tarvitsemme yhteiskuntasopimuksen siitä, mitä palveluita jatkossa tuotetaan verovaroin ja velaksi. Valtion korkomenoihin menee jo enemmän rahaa kuin kuntien peruspalvelujen valtionosuuksiin, tuhansia miljoonia euroja. Nämä rahat ovat poissa muualta, vanhushoivasta, lapsiemme koulutuksesta, terveydenhoidosta. Kasvua tulee toivoa, mutta kasvun varaan ei voi laskea. Suomessa talouskasvun esteeksi muodostuu lapsiemme heikkenevät oppimistulokset. Nyt on viimeinen hetki kääntää kurssi.

    Parlamentaariseen yhteiskuntasopimukseen ei kannata haaskata aikaa, eduskuntapuolueiden arvomaailmat ovat liian kaukana toisistaan. Vaalit antavat enemmistöhallitukselle legitiimin mandaatin käyttää valtaa. Avoin keskustelu 10 miljardin leikkauskohteista ennen seuraavia eduskuntavaaleja ovat paras korvike laajalle yhteiskuntasopimukselle.

  • Talouskasvupuheesta tekoihin

    Talouskasvupuheesta tekoihin

    KTT Risto Murron työryhmän kasvuraportti on julkaistu. Raportissa on joukko ehdotuksia. Osa niistä on varsin hyviä. Suomen talous on saatava kasvuun 17 kitukasvuisen vuoden jälkeen. Joka tapauksessa hyvästäkin kasvusta huolimatta on todennäköistä, että seuraavakin hallitus joutuu sopeuttamaan noin 10 miljardia valtiontaloutta seuraavan vaalikauden aikana. Puolustusmenojen raju kasvu pitää kompensoida sopeuttamalla muualta. Veroja ei kannata kiristää enää kokonaisuutena, rakennetta voi optimoida. Veronalennusvara pitää käyttää optimaalisesti. Onneksi verotus on kokonaisuutena kevyempää verrattuna 1990-luvun loppuun. Toisaalta eläkemaksut tappavat meillä kasvua. Väestörakenne on iso kansantaloudellinen ongelma, ja siihen ei auta kehitysmaamaahanmuutto lieveilmiöineen. Ympyrä on hankala neliöidä. Ehkä varustelukierre johtaa talouskasvuun.

    Taloudellinen kasvu tarkoittaa sitä, että bruttokansantuote kasvaa reaalisesti, ja vielä mielellään niin, että henkeä kohti laskettu reaalinen bruttokansantuote kasvaa. Reaalinen kasvu tarkoittaa sitä, että tuotannon volyymi kasvaa. Kansantaloustieteessä kasvuteorian kivijalka on toisaalta Ramseyn kasvumalli vuodelta 1928 (sekä Cass-Koopmans 1965, kuluttajan dynaaminen optimointitehtävä), toisaalta neoklassinen Solow-Swan – kasvumalli vuodelta 1956. Sittemmin on esitelty endogeenisen kasvun malleja, joissa on mukana inhimillinen pääoma. Ei mennä niihin tässä syvälle, mutta pari sanaa kuitenkin.

    Kasvu teoriassa?

    Bob Solowin kasvumallissa oletetaan, että kokonaistuotanto Y riippuu reaalisen pääoman määrästä K (koneet, laitteet), toisaalta työpanoksen määrästä L, sekä teknologiasta A. Siten voimme kirjoittaa tuotannon funktion Y=F(A,K,L). Solowin mallissa oletetaan, että pääoman ja työn rajatuottavuus on laskeva. Lisäksi oletetaan muita teknisiä ominaisuuksia tuotantofunktiolta F. Tämän kirjoituksen kannalta olennainen mallin ennuste on se, että ilman teknologian kehitystä per capita – kasvu pysähtyy lopulta. Teknologian kehitys on siis välttämätöntä pitkän aikavälin talouskasvun kannalta. Teknologia tarkoittaa käytännössä innovaatioita. Siis pelkät investoinnit eivät riitä, vaan tarvitsemme teknologista kehitystä ja uusia tuotteita, uusia laitteita, uusia koneita. Pääoma kasvaa investoinneista, ja investoinnit seuraavat innovaatioita. Matala korkotaso auttaa investoinneissa.

    Teknologian kehitys talouskasvun kannalta tarkoittaa mallissa sitä, että samalla pääomakannalla ja samalla työpanoksella saamme aikaan suuremman tuotannon. Eli jos meillä on vaikka 100 ihmistä tehtaassa ajamassa jotakin tuotantoprosessia, niin tuotos voi vaihdella käytössä olevan teknologian mukana. Tämä voi tarkoittaa yksinkertaistaen vaikkapa sitä, että moottorit ovat tehtaissa tehokkaita, lopputuotteesta ollaan valmiita maksamaan paljon maailmanmarkkinoilla, ja tuotantoprosessit ovat optimaalisia. Lisäksi teknologian voi ymmärtää myös yksinkertaistaen niin, että työntekijät saavat enemmän aikaan annetulla pääomakannalla. Teknologia on mielletty juuri osaksi työpanoksen tuottavuutta osittain siksi, että se takaa Solowin mallissa tasapainon.

    Suomi nousuun

    Nykyisin ekonomistit puhuvat paljon työn tuottavuudesta ja sen heikosta kasvusta Suomessa. Jos selitämme talouskasvua vain työpanoksella, on todella niin, että työn tuottavuuden kasvu on ollut heikkoa. Meidän pitäisi saada korkean jalostusasteen vientiä lisää. Soveltavia ratkaisuja ihmisten tarpeisiin, uusia innovaatioita. Esimerkiksi taistelurobotteja tai tekoälyrobotteja siviilikäyttöön. Toisaalta uudet innovaatiot metsäteollisuudessa ja konepajateollisuudessa voivat täydentää näitä uusia kasvualoja. Ilmastoteknologia on mahdollisuus. Oma kysymyksensä on esimerkiksi kvanttilaskenta ja uudet tekoälymallit, tai vastaavat korkean teknologian tuotteet. Teollisuuspolitiikka voi tukea innovaatioita ja TKI-toimintaa. Suomessa TKI:n alalle on satsattu viime vuosina paljon julkista rahaa. Tarvitsemme kuitenkin ennen muuta lisää yksityisiä TKI-panostuksia – se onkin julkisen rahoituksen edellytys. Bell Labs on tästä hyvä esimerkki. Bell Labs on Nokian omistama aivokeskus. EU:n alueella toimivat puolustusvoimat voisivat ehkä perustaa ýhteisen vastineen amerikkalaiselle DARPA:lle.

    Tarvitsemme siis pysyvää teknologian kehitystä, jos mielimme pysyvää talouskasvua. Reaalinen talouskasvu auttaisi painamaan velkasuhdettamme alas, esimerkiksi. Kasvu vähentäisi sopeutustarvetta merkittävästi. Lisäksi voisimme työskennellä teoriassa vähemmän. Talouskasvu on siis hyvä asia. Toki ympäristön tuhoutumista tulisi pyrkiä minimoimaan samalla. Suomen olosuhteissa pitäisi myös saada väestörakenne terveemmäksi. Suomalaisten pitäisi alkaa tehdä lapsia vähintään 2 per pariskunta. Jokin verokannuste voisi auttaa tässä.

    Innovaatiot ovat satunnaisia?

    Teknologian kehitys on ollut jatkuvaa. Tuli otettiin käyttöön jo 500 000 ekr. Metsästäjä-keräilijät siirtyivät maanviljelyyn noin 15 000 ekr. Tämä mahdollisti kaupungistumisenkin. Pyörä keksittiin Irakissa noin 3 300 ekr. Roomalaiset ottivat käyttöön vesirattaan viljan jauhamiseksi vuonna 101 ekr. Vuonna 50 jkr. Heron keksii ensimmäisen höyrykoneen. Vuonna 620 intialainen matemaatikko Brahmagupta kirjoittaa kirjan negatiivista luvuista. Vuonna 700 tuulimylly keksitään Iranissa. Johannes Gutenberg painaa vuonna 1454 ensimmäisen kirjan. Tieteellinen vallankumous pääsee vauhtiin 1600-luvulla, ranskalainen filosofi Rene Descartes muotoilee tieteellisen menetelmän ja väittää valon olevan aaltoliikettä. Fyysikko ja alkemisti Isaac Newton kehittää mekaniikan perustan ja Newtonin lait (1687). Yleisnero G.W. Leibniz keksii mekaanisen tietokoneen ja binääriluvut. Thomas Newcomen rakensi ensimmäisen kunnon höyrykoneen jo vuonna 1705. James Watt paransi oleellisesti konseptia vuonna 1780. Mekaniikan alalla Leonhard Euler, Joseph-Louis Lagrange ja William Hamilton muotoilivat analyyttisen klassisen mekaniikan. USA:ssa Benjamin Franklin tutki sähköä. Michael Faraday keksi sähkömagneettisen induktion 1831 Englannissa. Maxwell muotoili sähkömagneettisen kenttäteorian 1860-luvulla, ja radioaallot löydettiin pian tämän jälkeen (Heinrich Hertz, 1888). Puhelin, radio keksittiin molemmat jo 1800-luvulla. 1900-luvulla keksittiin transistorit, integroidut piirit ja mikroprosessorit. Atomipommit, ydinreaktorit ja avaruusraketit. Tieteellinen liikkeenjohto tuli muotiin. Monet näistä megainnovaatioista ovat syntyneet yliopistojen ulkopuolella, yksityisten pellepelottomien kammareissa. Luovuus ja hulluus kulkevat monesti käsi kädessä.

    Tekniikka ja luonnontieteet ovat välttämättömiä ihmiskunnan kehityksen kannalta. Lääketieteen avulla inhimillistä kärsimystä on vähennetty hurjasti. Fysiikka, kemia ja tekniikka perustuvat kaikki matematiikkaan. Lääketiede ja biologia hyödyntävät tieteellistä menetelmää. Kaikki luonnontieteet ovat jollakin tapaa hyödyllisiä talouskasvunkin kannalta.

    Opin sauna, autuas aina.

    Teknologia on siis kallisarvoista. Teknologian kehitys perustuu koulutukseen ja oppineisuuteen. Lapsien tulee osata riittävästi matematiikkaa ja luonnontieteitä peruskoulussa, jotta lukioissa ja ammattikouluissa voimme antaa eväitä jatkoon. Yliopiston perustutkimus tuottaa luonnontieteissä arvokasta tietoa. Innovaatiot syntyvät usein kuitenkin satunnaisemmin. Panostukset tutkimukseen ja tuotekehitykseen voivat auttaa, mutta tärkeämpää Suomessa on vaatia lapsiltamme laskutaitoa, lukutaitoa, kirjoitustaitoa. Ei voi kehittää fuusiota, jos ei hallitse perustaitoja. Tekoälykin nojaa matematiikkaan ja tilastotieteeseen. Kvanttilaskenta perustuu matematiikkaan. Ydinreaktorin neutronivuota mallinnetaan osittaisdifferentiaaliyhtälöillä. Sähköä syntyy, koska Maxwellin yhtälöt kertovat sen meille. Luonto on valjastettu ihmiskunnan hyötykäyttöön. Rikastusuuneissa tarvitaan energiataselaskentaa. Uudessa maailmassa pärjää vain kovalla osaamisella. Ei tehdä lapsillemme karhunpalvelusta.

    Suomalaisissa kouluissa on rauhatonta ja oppimistulokset laskevat. Mistä tulevat seuraavat AIV-rehun keksijät, tekstiviestin keksijät, uudet Linuxit? Olemme huolestuttavassa kierteessä. Oppimistulosten oikaisemiseksi tarvitsemme ryhtiliikkeen ja asennemuutoksen. Kännykät pois luokista, kuri ja auktoriteetti takaisin. Muuten tulevaisuuden Leena Palotiet, Teuvo Kohoset ja Rolf Nevanlinnat jäävät kasvamatta.

    Seiniä on tarpeeksi – pellepelottomia liian vähän

    Suomessa investointien laatu on muuttunut vaikkapa 1990-luvun lopulta tähän päivään, nykyisin investoidaan enemmän seiniin ja rakennuksiin, ennen koneisiin ja laitteisiin. Jos ajattelemme tuotantofunktiota Y=F(K,L,A), koneet ja laitteet edustavat K-panosta. Investoinnit uusiin koneisiin toisaalta ovat innovaatioiden ja teknologian uudistumisen seurausta. Esimerkiksi, kun jokin kemianteollisuuden yritys kehittää uuden kemikaalin, yritys rakentaa sen ympärille uuden prosessiteollisuuden tuotanto- ja arvoketjun logistiikkoineen ja markkinointeineen. Joka tapauksessa tarvitsemme investointeja, joita edeltää innovaatiot ja teknologian kasvu. Lisäksi tarvitsemme korkean jalostusarvon tuotantoa, emme halua pelkkiä kaivoksia tai datakeskuksia. Suomessa voisi olla mahdollisuuksia esimerkiksi yhdistellä automaatiota, robotiikkaa, puolustusteollisuutta, tekoälyä. Vetytalouden ympärille voi syntyä ammoniakkiteollisuutta, typpihappoa, trinitrotolueenia. Räjähtävään kasvuun! Poriin on tulossa iso TNT-tehdas.

    TKI-rahoituslaki takaa riittävän rahoituksen Suomessa toistaiseksi, mutta on entistä tärkeämpää kohdentaa rahoitus optimaalisesti. Itse suosisin soveltavaa tutkimusta luonnontieteen alalla. Lääketeollisuus on myös potentiaalinen kasvunala. Meillä ei ole varaa tutkia kaikkea. Pienen maan tulee priorisoida ja ottaa riskiä. Aika näyttää, miten rahoituslaki poikii innovaatioita. Tarvitsemme myös Kari Kairamon maanisuutta myyntiin ja markkinointiin, Jorma Ollilan visiota, ja Pentti Kourin älyä. Suhdanneseminaarit takaisin! Yliopistojen ja innovaatiomyönteisten firmojen synergiaa on vahvistettava. Kasvukiihdyttämöt ovat hyvä juttu, ja varsinkin Otaniemessä on hyvää pöhinää. Riskirahoitusta tulee olla saatavilla.

    Voisiko opettajille ja oppilaille kehittää jonkinlaisen tulospalkkausmallin? Jos mittaamme objektiivisesti lukemista, laskemista ja matematiikan taitoja, voisivat hyvin pärjänneet luokat saada jonkinlaisen palkinnon tai kannustimen. Hyvät tulokset voisivat näkyä opettajan tilipussissa. Yliopistojen rahoitusmomentilla on rahaa paljon, ehkä sieltä löytyisi tarvittava bonus? Akateemisesta vapaudesta voisi samoin luopua tuottavuuden parantamiseksi. Tyrnävän Kuulammen koulun malli pitäisi skaalata koko maahan. Fiksut tasoryhmät siis takaisin. Varusmiespalveluksen P1- ja P2-testien perusteella voisi poimia ikäluokasta terävää porukkaa vaikka armeijan start-up -hautomoon. Israelissa on tällainen malli, innovatiivisen Yozma-kasvurahoitusmallin ohella. Sivarissakin on fiksua porukkaa, nämä lahjakkuusreservit kannattaa tunnistaa. Business Finlandin ja Teollisuussijoituksen resurssit pitää optimoida.

    Itävaltalainen taloustieteilijä Joseph Schumpeter piti yrittäjiä innovaatioiden ajureina. Näin todella on. Yrittäjät ovat kansantalouden sankareita. Luova tuho karsii vanhaa teknologiaa ja pääomakantaa. Uutta syntyy. Laittamalla perustukset kuntoon saamme Suomen kyllä vielä kasvun uralle!

  • Miksi olen konservatiivi?

    Miksi olen konservatiivi?

    Amerikkalainen kirjailija Hunter S.Thompson (1937-2005) on antanut meille lentävän lauseen, vapaasti mukaillen: ”Kun hommat menee oudoksi, oudoista tulee ammattilaisia.”. Tämä ajatus sisältää paljon totuutta tässä ajassa. Nykyisin monet pitävät esimerkiksi konservatiivista ajattelua outona, vaikka ennen se oli normaalia. Väitän, että keksimme pian siis maalaisjärjen legitiimisti uudelleen. Olen yrittänyt pohtia syytä, miksi pidän tätä aikaa outona, hullunakin, ja luulen, että en ole ajatuksineni yksin.

    Synnyin Kuopiossa, kylmänä tiistai-iltapäivänä, kesäkuussa 1982. Asuimme omakotitalossa Siilinjärvellä. Kotitaustani on keskiluokkaa, emme olleet varakkaita, koulutusta arvostettiin. Lapsuuteni 1980-luvusta muistan eritoten Tsernobylin ydinvoimalaonnettomuuden, Hymyhuulet –sketsisarjan ja kuumat, mannermaiset kesät. Kesät olivat pitkiä ja täynnä lapsenmielisen ihmisen ihmettelyä kaikesta uudesta. Poltimme ruutupaperia suurennuslasilla, leikimme kielletyillä rakennustyömailla. Saimme satikutia, kasvoimme ihmisiksi, aikuisiksi. Taloudellinen suhdannekin oli kasinotalouden luottokuplan ansiosta lapsuudessa hyvä aina lamavuosiin saakka. Isällänikin oli sellainen iso, kiloja painava autopuhelin. Kylmän sodan ydinaseuhkaa ei pieni lapsi osannut pelätä. Neuvostoliitosta sai kuulla ilta-uutisissa, väritelevisiosta. Tietokoneen sain vuonna 1990, muistaakseni. Olisi pitänyt ohjelmoida, pelasin, mutta opin englantia.

    Vaikka lama-aika oli yleisesti ottaen ankeaa, ei se kuitenkaan osunut kovinkaan pahoin perheeseemme. 1990-luvun alku oli minulle duurivoittoista aikaa, ja koko 1990-luku oli kokonaisuutena optimismin täyttämää. Muistan muurin murtumisen 1989, samoin Neuvostoliiton hajoamisen ja IVY:n. Kylmän sodan vuosien jälkeen Suomi kiinnittyi länteen, haimme EU-jäsenyyttä nopeasti, Suomi osti Hornetit ja R-kioskeista sai vuokrata amerikkalaisia toimintaelokuvia, VHS-videoita. Poliittinen satiiri oli sallittua, ja sketsiohjelmat olivat oikeasti hauskoja. Televisioon ei ollut vielä iskenyt taannehtiva sensuuri. Iltalypsyä katsoin paljon.Tabuja oli vähemmän, asioista sai puhua vapaammin ilman painostavaa oikeamielisten sensuurin varjoa.

    1990-luvun henkistä ilmapiiriä leimasi toivorikkaus, edistyksellisyys ja usko paremmasta maailmasta. Vain taivas oli rajana, tulevaisuus oli avoin ja täynnä mahdollisuuksia. Kilpailu oli kovaa, mutta peli oli reilua. Kokeisiin piti lukea viimeistään lukiossa. Lukiosta piti saada hyvät arvosanat, jotta saisi kunniallisen ja kohtuullisesti palkatun ammatin. Nuoruuden odottavan mielen valossa tässä nostalgiassa varmaankin osin aika on kullannut muistoja. Toki silloinkin oli sosiaalisia ja taloudellisia ongelmia, mutta ihmiset olivat mielestäni jotenkin tolkullisempia ja realistisempia, juurtuneita todellisuuteen.

    Pikkuhiljaa maailma muuttui, ja kulttuuri normeineen muuttui. Sosiaalinen media ja internet ovat tuoneet ison kaikukopan vastakkainasettelulle, kärjistämiselle. Määrätynlainen suvaitsemattomuus ja ajatusfundamentalismi on lisääntynyt. Olet joko oikeassa tai väärässä. Spektri ja vivahteet ovat unohtuneet, maailmassa on myös harmaan sävyjä. Olet rasisti tai antirasisti. Kolonialisti tai vapaustaistelija. Riistäjä tai riistetty. Syy löytyy aina ulkopuolelta, taloudellisen tehokkuuden maailmassa myös vastuu omasta elämästä on yhtiöitetty ja ulkoistettu. Syynä ovat rakenteet tai sorto, yhteiskunnassa on vika, yhteisössä. Ihmisen vastuu itsestään on unohtunut. Vaikka yläasteen päättäjäispuheeni loppusanoissa ”Jokainen on oman onnensa seppä.” on aimo annos infantiilia idealismia, pitää lause edelleen ainakin puoliksi paikkansa. Ihmisen on otettava itsestänsä vastuu. Työpaikat ja opiskelupaikat pitää ansaita, niitä varten on puurrettava ja tehtävä töitä. Se ei ole aina pelkkää ruusuillatanssimista.

    Nykyisessä eetoksessa on vain oikeuksia, vailla velvollisuuksia. Valtiosäännön tosiasiallinen tulkinta on vinoutunut. Kun Karl Marxin ajatusrakennelma ei kestä loogis-analyyttistä tarkastelua, ja virheellisen lisäarvoteorian johdosta (modus ponendo ponens) koko kommunismin teoriakehikko romahtaa, on vasemmiston älyllinen tyhjiö ollut pakko täyttää jollakin uudella. Suunnitelmatalouden ja suoran sosialismin on korvannut antikolonialismi, antirasismi, osin myös överiksi mennyt ja sisäisesti ristiriitainen ympäristöliike sekä telaketjufeminismi.

    Listaa voi jatkaa. On woketusta, cancelointia, kulttuurirelativismia, ylinumeroituvasti ääretön määrä sukupuolia, unisex-vessoja ja niin edelleen. En halua käydä naisten kanssa vessassa. Valkoinen, länsimainen heteromies on pahuuden lokuksessa, fokuksessa. Maskuliinisuudesta ja protestanttisesta eurooppalaisen miehen symbolista on tullut syntiä. On hävettävä, jos edustaa perityypillistä maskuliinista perusmiestä, WASPia. Mies on syyllinen ja sortaja. De-maskulinisaatio tarkoittaa sitä, että sukupuolisuus pyritään häivyttämään, neutraloimaan. Marxilaisen lisäarvo- ja riistoteorian on korvannut äärimmäisyyteen viritetty lopputulosten tasa-arvo. Papisto johtaa puhetta, ja lauma hymistelee ja resonoi. Vulgäärisosialismissa ei ole yksilöllisiä kivijalkakauppoja, on Kauppa ja Apteekki. Ravintola. Erillisyys poistetaan, on vain edistyksellisen woke-sosialismin tietotoimiston määrittämä virallinen totuus.

    Virallisen papiston totuuden pahin uhka on sananvapaus, analyyttinen keskustelu ja kyseenalaistaminen. Mikään totalitaristinen tai huono ideologia ei kestä analyyttista tarkastelua, siksi säännönmukaisesti kaikissa totalitaristisissa ideologioissa kielletään ensimmäiseksi tiedon vapaa välitys. Vapaa debatti karsii huonot ideat pois jatkosta, eräänlaista tieteellistä prosessia ja evoluutiota, siis. Avoin yhteiskunta vaatii kuitenkin puolustajansa.

    Nuoruudessani 1990-luvulla moni asia oli huonommin, se on myönnettävä. Naisten oikeudet ovat menneet pääosin hyvään suuntaan, ja seksuaalivähemmistöjen asema on samoin melkoisen hyvä nykyisin. Talous ei ole kasvanut Suomessa tosin finanssikriisin jälkeen, mutta toisaalta ei meillä ollut iPhonea ja Olkiluoto 3:sta vielä vuonna 2005. Reserviupseerikoulun viikonloppuvapailla Helsingissä luin sähköpostit mBarin julkisesta internet-päätteestä. TKK:lla oli unix-pääte. Hyvin pärjättiin silloinkin. Naiset olivat kauniita tuolloinkin, opiskelijaruoka oli hyvää, keskusteluilmapiiri oli jotenkin terveempi ja avoimempi. Vallitsi vapauden ilmapiiri. Valtiotieteellisessä tiedekunnassa, Kuppalan bileissä puhuttiin politiikkaa. Oltiin eri mieltä, mutta ilmapiiri ei ollut hostiili tai vihamielinen. Vasemmistolaiset poliittisen historian opiskelijat kykenivät sivistyneeseen ja älykkääseen debattiin oikeistolaisten kansantaloustieteilijöiden kanssa. Tosin vallankumouksesta varmaan silloinkin moni haaveili. Nykyisin valtsikan bileet ovat varmaankin melko kliinisiä. Turvallisessa tilassa pitää puhua vain aiheista, jotka eivät loukkaa ketään taikka muutoin ole epämiellyttäviä tematiikaltaan.

    Totalitaristiseen eetokseen liittyy sensuuri, jota EU:kin näyttää edistävän uusien komissaarien suulla. Näennäissivistynyt tapa kieltää vihapuhe, ja korvata se kivapuheella on kulttuurirelativismia. Kun kaikki asiat ovat yhtä hyviä, kriitiikkiä ei tarvita. Kaikilla on kliffaa. Suomalaista liberaalia oikeusvaltiota ei saa asettaa arvoasteikolla paremmaksi muihin kulttuureihin nähden. On toki niin, että suomalaista kulttuuria saa morkata, ja meidän kulttuurimme joutaa sopeutua. Uimahalleissa mennään maahanmuuttajien ehdoilla. Nöyristelemme, pyytelemme anteeksi. Olemme hissukoita. Elämme kollektiivisen itsehäpeän aikaa.

    Nöyristelyn lisäksi velttoilemme. Tämä näkyy jo peruskouluissa, missä oppilaat päästetään luokalta vailla laskutaitoa. Elämme myös kollektiivisen itsepetoksen aikaa. Ajattelemme, että naisvihamieliset primitiivikulttuurit assimiloituvat ja integroituvat suomalaiseen tapakulttuuriin. Se, että integraatio ei ole onnistunut yhdessäkään eurooppalaisessa maassa, ei lannista monikulttuurisen sosiaalisen oikeudenmukaisuuden woke-sotureita. Lappikin on nykyisin Kongon veroinen siirtomaa wokettajien ajatuksissa. Afrikan tähti ja Peppi Pitkätossu ovat Danten helvetin sisäkehien seurapelejä. On tämä hullua aikaa!

    Onneksi on toivoa. Historiaa katsomalla näemme säännönmukaisuuden: hullutukset tulevat ja menevät. Usein on niin, että hullutusta kestää aikansa, lopulta huomataan että keisarilla ei ole vaatteita, ja tulee rekyyliliike. Tasapaino löytyy lopulta. Locken ja Smithin liberalismin ideaali ei voi olla nykyinen wokehumppa. Jos Popper eläisi, hän olisi varmaankin pahasti masentunut. Liberalismin ideaaliin täytyy kuulua se, että ikävistä asioista voidaan keskustella. Suomalainen kulttuuri on hyvä, parempi moniin muihin verrattuna. Ei kannibalistisia kulttuureja hyväksytty edes löytöretkien aikaan. Suomalainen liberaali oikeusvaltio on syntynyt evolutiivisen prosessin kautta. On koeteltu julkisesti erilaisia ideoita. SDP:n osallistuminen marxis-leninistiseen punakapinaan on suuri häpeätahra muutoin suhteellisen salonkikelpoisessa poliittisessa historiassamme. Anders Chydenius (1729-1803) kehitti liberaaleja ajatuksia jo ennen skottivalistusta, ajatella täällä Pohjan perällä! Jo vuosisadan alussa teoreettinen fyysikko Gunnar Nordström (1881-1923) kehitti painovoimateoriaa ja yhtenäisteoriaa sähkömagnetismin ja gravitaation osalta. Leo Mechelin, Eino Kaila, von Wright, Jaakko Hintikka. Karjalainen käänsi Keynesin Yleisen teorian. On ollut sivistystä. Meillä oli joskus jopa sellainenkin, mitä kutsuttiin älymystöksi. Kriitikko Seppo Heikinheimon (1938-1997) sanoin nykyisin pesäpallo-otteluissakin kuunnellaan vaan ”mökämusiikkia”. Mökämusiikin jatkeeksi olemme myös korvaamassa Suomen kielen. Häpeämme ja nöyristelemme siinäkin.

    ”Oikeamielisen” wokepapiston suuri tragedia, ironiakin, on se, että oikeamielinen överisuvaitsevaisuus tuhoaa lopulta itsensä. Primitiiviset totalitaristiset aatteet valtaavat alaa Euroopassa. Sileäkätinen woke-papisto ei pärjää tässä uudessa vihamielisessä maailmassa. Kulttuurievoluutiossa heikko, lopputulosten tasa-arvoa, överifeminismiä ja woketusta edistävä totalitarismi häviää toiselle totalitarismille. Jo heikko syntyvyys Suomessa takaa tämän, jos ei muu. Olisi aika ryhtyä itsesäilytystalkoisiin, kulttuurin ja itsemme osalta.

    Tervehenkisessä yhteiskunnassa on tolkku, maltti, kohtuus, maalaisjärki. Ydinperheellä on ensisijainen kasvatusvastuu. Miehet saavat olla miehiä, ja maskuliinisuus ei ole syntiä. Armeijan käyminen on oikeus ja velvollisuus. Naiseus tulee naisilla muotiin. Yhteiskunta, jossa kotikasvatuksen on korvannut Tik-Tok, ja luokkahuoneissa eletään kuin pellossa, kasvaa valtionkin konkurssin siemen.

    On aika todeta ääneen: tarvitsemme arvoja, jotka meillä ovat olleet satoja vuosia. Siis konservatismia. Nämä arvot ovat olleet pois muodista 20 vuotta, mutta ne ovat kestäneet silti tuhansia vuosia – niitä on koeteltu. Siksi olen optimistinen. Tulee vielä aika, jolloin opettajilla on auktoriteetti, naiiville maahanmuuttopolitiikalle tulee stoppi, ja konservatismista tulee taas muotia. Yhteiskunta löytää kestävän tasapainon yritys-erehdys –prosessin kautta. Valitettavasti, jos kollektiivinen järjen valo ei syty pian, asiat menevät huonompaan suuntaan ennen käännöstä. Lukutaidottomat raggarit riehuvat kaduilla, jengeissä. Sosiaalituilla elää pian valtaisa post-moderni paarialuokka. Valtio ylivelkaantuu ja hukkuu löysään vetelehtimiseen – tähän vetelehtimiseen osallistuvat kaikki Suomessa, toiset enemmän kuin toiset. Työnteko ja oppiminen kun ei ole kivaa, ja totuudenpuhujista ei tykätä. Ikävistä tosiasioista kun voi joku loukkaantua! Moni on varmasti samaa mieltä siitä, että elämme jonkinlaista kollektiivisen hulluuden aikaa, mutta ei uskalla sanoittaa ajatuksiaan ääneen. Kuitenkin on välttämätöntä puhua Suomen, ja laajemmin Euroopan ongelmista.

    Vetelehtimiskulttuuri muuten liittyy ajallisesti tähän uuteen talousjärjestykseemme myös. Bretton Woods – järjestelmän ja kultakannan romahtaminen on johtanut siihen, että vetelehtiminen on helppoa. Koska velkaantuminen on helppoa. EU ja euro on pahentanut ongelmaa, riskilisät ovat menneet valtionlainoissa nippuun, koska sijoittajat uskovat lopulta johonkin pelastuspakettiin. Siis taloudellinen ja institutionaalinen järjestelymme on osaltaan ruokkinut tätä laiskuuden aikaa. Työ ei ole perusoikeus, se on ansaittava. Pitää osata jotakin, josta joku on valmis maksamaan. Koulussa pitää oppia lukemaan, laskemaan ja kirjoittamaan. Vanhempien pitää asetttaa lapsille rajat.

    Sananvapaus on uhattuna. Kaikkien itseään kunnioittavien ja ajattelevien ihmisten on ryhdyttävä puolustamaan sitä. Muuten olemme tiellä orjuuteen. Sananvapauden säilyessä woketukselle ja muulle sekoilulle tulee peräseinä vastaan, ja yhteiskunnallinen eheytyminen kohti terveempää yhteiskuntaa voi alkaa. Haluan tuoda lapsuuteni Suomesta parhaat osat takaisin, tolkullisuuden, sivistyksen, reippauden. Jos 2000-luvun suurin muutos on tämä sensuurikulttuuri ja loukkaantumiskulttuuri, pärjäisin vallan hyvin 1990-luvun materiaalisellla tasolla. Lopulta materialistinen kulutus on hyvinvointivaikutuksiltaan loputonta kilpailua. Ihmiset vertaavat aina kulutustaan ja krääsän määrää muihin. Minulla on hienompi auto, vene jne. Vähemmälläkin pärjäisin itse, jos saisin vaihtokauppana vapaan ja avoimen yhteiskunnan, turvalliset kadut, vähävelkaisen valtion, laskutaitoiset aikuiset ja sekavuorot uimahallissa.

  • Helsingin kaupungin talous – missä mennään näin kuntavaalien alla?

    Helsingin kaupungin talous – missä mennään näin kuntavaalien alla?

    Kuntavaaliehdokkaalla täytyy olla edes auttava tai alustava käsitys kotikuntansa tai –kaupunkinsa taloudenpidosta. Kuntapolitiikassakin talous on toiminnan perusta ja rajoite. Kaupungilla on budjettirajoite, kuten valtiollakin. Helsingin tilanne on ainutlaatuinen, koska sotepe-palveluiden (sosiaalihuolto, terveyspalvelut, pelastus) järjestämisvastuu on edelleen kaupungilla Helsingin erityisratkaisun vuoksi. Erikoissairaanhoito toteutetaan HUS-yhtymään osallistumalla. Helsingin kaupungilla on lakisääteinen velvollisuus kuulua HUS-yhtymään.

    Toisaalta Helsinki on muuttovoittokunta verrattuna vaikkapa moniin maakuntien kuntiin Suomessa. Aika näyttää, ovatko maahanmuuttajat nettohyötyä kaupungin taloudenpidon kannalta. Itä-Helsinki on pahalla segregoitumisuralla. Koulushoppailu jatkaa suosiotaan, koulurauha vaihtelee alueittain. Alueiden eriytyminen voimistunee, sama trendi on suuressa osassa eurooppalaisia kaupunkeja. Tähän toki voi politiikalla vaikuttaa! Tästä syystä osin olen ehdokkaana.

    Talouden tunnuslukujen kursorisella tarkastelulla ei vielä voi päästä käsiksi siihen, käytetäänkö veronmaksajan rahaa parhaalla mahdollisella tavalla, optimaalisesti. Kuntapäättäjien tehtävä on pitää huolta kuntalaisten ja veronmaksajien edusta, vaikka kaupungin johto operatiivisesti hoitaa oman tonttinsa. Siksi asioita pitää selvittää, ja niihin tulee perehtyä. Myös tällaisiin kuiviin talousasioihin. Talouden ymmärtäminen antaa eväät fiksulle ja vastuulliselle kuntapolitiikalle.

    Helsingin poikkeavan sote-ratkaisun vuoksi kaupunki raportoi tilinpäätöstiedoissa erillistilinpäätökset koko kaupungin, kunta-Helsingin ja sotepe-Helsingin osalta. Lisäksi on tarjolla yhdisteltyä konsernitietoa. Helsingillä on paljon yhtiöomistuksia ja –osuuksia.

    Tutustuin Helsingin kaupungin vuoden 2023 tilinpäätökseen. Helsingin tilanne on kokonaisuutena pintapuolisesti arvioiden suhteellisen hyvä. Tarkastelen tässä lyhyesti kunta-Helsinkiä ja sotepe-Helsinkiä erikseen. 

    Konsernitarkastelussa kiinnitän tässä huomiota siihen, että velkaa on noin 7 miljardia, ja investointimenoja varten otetaan lisää uutta nettovelkaa noin 600 me toiminnan ja investointien rahavirran perusteella. Konsernitarkastelussa näkyy kaupungin yhtiöomistus mm. asunto- ja energiantuotannossa (Helen) investointitarpeineen jne.

    Kunta-Helsinki

    Kuntataloutta tutkiessa katson ainakin toimintakatteen, eli nettomenot, vuosikatteen, jossa mukana verot ja valtion rahoitus sekä rahoitustuotot ja –kulut. Lisäksi varsinainen tulos kertoo mitä jää viivan alle poistojen, arvonalentumisten ja satunnaisten erien jälkeen. Vuosikate kertoo ennen muuta käyttötaloudesta.

    Kuten laajemminkin elinkeinotoiminnassa, vuosikatteen pitäisi ensinnäkin riittää kattamaan juoksevat käyttötalouden menot. Lisäksi vuosikatteen tulisi riittää kattamaan poistot, kun investoinnit on aktivoitu esim. käyttöomaisuuden hankintamenona taseeseen. Näin ollen tilikauden tulos on aivan relevantti tunnusluku myös kuntataloudessa. Toki kunnat eivät sinällään tavoittele voittoa, ja raha- ja reaaliprosesseissa on omat nyanssinsa. Likviditeettiin tai kaupungin maksuvalmiuteen en tässä kiinnitä suurta huomiota.

    Kunta-Helsinki kerää verotuloja yli 2 miljardia euroa vuosittain, ja saa valtionosuuksia noin 200 miljoonaa euroa. Nettomenot olivat 1,6 miljardia euroa.

    Kunta-Helsingissä vuosikatteen suhde poistoihin on hyvä, yli 220 prosenttia, kunta-Helsingin tilikauden tuloskin oli melkein puoli miljardia euroa vuonna 2023. Toki kunta-Helsingillä on miltei miljardi velkaa, kaupunkikonsernilla yli 7 miljardia. Velka ei ole sinänsä paha, jos sitä ei ole liikaa, ja se käytetään järkeviin, tuottaviin investointeihin. Investoinnin riskikorjatun tuotto-odotuksen tulee ylittää uuden velan odotettu riskikorjattu kustannus. Taseeseen kertynyt ylijäämä on yli 7,7 miljardia euroa, eli kunta-Helsingin tulorahoitus on ollut riittävää historiallisesti.

    Rahoituslaskelmapuolelta kunta-Helsingin toiminnan ja investointien rahavirta vuodelta 2023 on noin 23 miljoonaa euroa plussalla. Toiminnan ja investointien rahavirran määrä  ilmaisee sen, kuinka paljon rahavirrasta jää nettoantolainaukseen, lainojen lyhennyksiin ja kassan vahvistamiseen. Negatiivinen määrä kertoisi siitä, että menoja jouduttaisiin kattamaan joko olemassa olevia kassavaroja vähentämällä taikka ottamalla lisää lainaa.

    Yksinkertaistettuna toiminnan ja investointien rahavirta kertoo negatiivisena paineen lainakannan kasvattamiseen tai veroprosentin korottamiseen ja positiivisena laskennallista mahdollisuutta muun muassa lainojen lyhentämiseen tai veroprosentin alentamiseen.

    Konsernitasolla Helsingin toiminnan ja investointien rahavirta oli noin 600 miljoonaa miinuksella vuonna 2023, eli investointeja on tehty paljon suhteessa vuosikatteeseen. Täällä siis näkyy myös yhtiöiden investointimenot yms. Toisaalta liukuvana summana tuo toiminnan ja investointien rahavirta konsernitasolla saattaa olla vahvempi.

    Kunta-Helsingin lainanhoitokate on erinomainen, eli tulorahoitus riittää hyvin lyhennyksiin ja korkoihin. Omavaraisuusaste on vahva, suhteellinen velkaantuneisuus kohtuullista.

    Kunta-Helsingissä siis tilanne taloudellinen tilanne on minusta hyvä kokonaisuutena.

    SOTE ja pelastustoimi

    Soten ja pelastuksen osalta juoksevien menojen pääasiallinen rahoitus tulee valtiolta hyvinvointialueuudistuksen myötä. Sotepe-Helsingin nettomenot olivat noin 2,6 miljardia euroa. Rahoitus oli suunnilleen samaa tasoa, joten sotepen osalta vuosikate jäi noin 40 miljoonaa plussalle vuonna 2023. Valtionrahoitus perustuu erilaisiin määräytymistekijöihin, kuten sairastavuuteen,  tarpeeseen ja asukaslukuun jne. Lisäksi siirtoa tasoitetaan siirtymätasauksella, joka on Helsingille positiivinen.

    Huomionarvoista on, että Helsingin sotepen valtionrahoitus kasvaa noin 250 miljoonaa euroa vuodesta 2024 vuoteen 2025, eli noin 9 prosenttia. Valtionrahoituksen määrän kasvuun vaikuttaa mm. siirtymätasaus ja vuoden 2023 tilinpäätöstietojen perusteella määräytyvä jälkikäteistarkistus koko maan tasolla, sekä lisäksi palveluntarvekorotus ja hintatason indeksikorotukset rahoituslain mukaisesti. Eli valtiolta tulee rahaa! Ja paljon!

    Vuoden 2023 tilinpäätöstietojen osalta sotepen nettokustannukset suhteessa valtionrahoitukseen ovat osuneet melko hyvin yksi yhteen. Jälkikäteistarkistus tehdään lain mukaan kuitenkin koko maan tasolla, joten Helsinki hyötyy nykymallista. Maakuntien alijäämät valuvat siis Helsingin ylijäämäksi jälkikäteistarkistusmekanismin kautta. Tämä on valitettavasti valtiontalouden kannalta yksi jumalaton menoautomaatti ja valuvirhe.

    Helsingin asukasperusteinen sotepe-kustannus on maan keskitasoa alhaisempi, mittakaavahyödyt auttavat tässä.

    Yhteenveto

    Kunta-Helsingin talous on likipitäen tasapainoinen ja tase on hyvässä kunnossa.

    Sotepe-puolella Helsinki hyötyy jälkikäteistarkistuksesta, kun maakuntien hyvinvointialueiden alijäämiä kapitoidaan koko maan tasolla Helsingillekin, vaikka Helsingin oma rahoitus ja nettokustannukset vastasivat hyvin toisiaan tilivuonna 2023.

    Konsernitason tarkasteluun en ehtinyt vielä paneutua, tässä katsoin vain kunta-Helsingin ja sotepen erillistilinpäätöksiä. Mutta yleisesti siis talous ei ole Helsingin suurin huoli.

    SOTEn puolella perusterveydenhoito on retuperällä ainakin jonotusaikojen perusteella. Kaupunginosien eriytymiskehitys ja koulujen rauhattomuus huolestuttaa.

  • Woketus ja ennakkosensuuri – case Afrikan tähti ja Peppi Pitkätossu

    Woketus ja ennakkosensuuri – case Afrikan tähti ja Peppi Pitkätossu

    Turun kaupunki on sosialidemokraattisen apulaispormestari Piia Elon (sd.) johdolla vakavasti ennakkosensuroimassa seurapelejä. Mainosmies Kari Mannerlan 1950-luvulla suunnittelemassa Afrikan tähti -seurapelissä jahdataan timantteja Afrikan mantereella. Aikansa kuvastolla. Sopimatonta lasten herkille sieluille – sensuuri iskee! Samoin saattaa käydä Peppi Pitkätossulle ja Viisikolle. Lastenkirjallisuus on tulilinjalla.

    Mikä tässä nyt sitten on ongelma?

    Ongelma on siinä, että kehityssuunta on erittäin vaarallinen, jos julkinen valta alkaa sensuroida vaikkapa erilaista kirjallisuutta vedoten siihen, että asianomainen kirjallisuus voi olla vaarallista mielipiteenmuokkauksessa. Jos Peppi, Viisikko ja Afrikan tähti on kolonialistinen ja sopimaton, mihin vedämme järkevästi rajan? Onko sopivaa luetuttaa lapsille ja nuorille Waltarin Sinuhe, egyptiläistä? Onko Sinuhe kolonialistinen primitiivisine kuvauksineen tuon ajan ihmisistä? Irwinin määrätyt renkutukset ovat wokesensuurin ensimmäinen kohde. Onneksi nuoremmat wokettajat eivät muista edes Raptoria. Entä poliittiset tekstit ja lopulta laajemmin oppositio? Valta tarvitsee vahtikoiransa. Siksi sensuuri on pahasta.

    On tietysti selvää, että se mikä on sopivaa, riippuu tulkitsijasta, ajasta ja kontekstista. Olisiko kuitenkin turvallisempaa varustaa erilaiset kammottavat seurapelit vain varoitustarroilla, ja mainita erikseen sanaston ja kuvaston olevan vaikkapa vanhanaikaista? Sensuuri voi johtaa pian muuhunkin kieltokulttuuriin. Paha arkipäiväistyy. Totalitaristiset ideologiat kumpuavat usein hyvistä aikomuksista. Mutta. Tie helvettiin on kivetty hyvillä aikomuksilla.

    Afrikan tähden mahdollinen cancelointi on esimerkki aikamme henkisestä syövästä, eli woketuksesta. Suomeen tulee usein Yhdysvalloista erilaisia muotivirtauksia, ja woketus ilmeisesti resonoi nuorissa vasemmistoidealisteissa ja sosiaalisen oikeudenmukaisuuden sotureissa kampuksilla ja aikanaan laajemmin yhteiskunnassa. Woketus on vaarallinen ja potentiaalisesti fasistinen ideologia, koska kielto- ja sensuurikulttuuri leviää helposti samoilla, kieroutuneilla argumenteilla. Kyse on osin myös massahysteriasta ja muoti-ilmiöstä.

    Osa woketuksen voimasta johtuu siitä, että ihmiset eivät uskalla nostaa kättä pystyyn, ja sanoa stop. Nostaa käsi pystyyn, ja todeta, ettei keisarilla totta vie ole vaatteita. Moni pelkää työpaikkansa tai sosiaalisen asemansa puolesta. Hiljaisuus ja vaikeneminen on helpompaa. Kuitenkin juuri näin pahat ideologiat pääsevät leviämään ja juurtumaan yhteiskuntaamme. On palattava maalaisjärkeen ja suhteellisuudentajuun.

    Wokemielisissä on vallalla jokin kollektiivinen syyllisyys – siitä sen on kummuttava. Suomen historia ei kuitenkaan tule kumpujen yöstä – meillä ei edes ollut siirtomaita. Erillissotakin oli välttämättömyys.

    Woketuksen vastakohta on sananvapauden ideaali. Sananvapaus tarkoittaa ideoiden ja ajatusten kilpalaulantaa. Parhaat ideat selviävät ajan testistä. Woketus ja sensuuri on taas raa’an voiman käyttöä ja toisinajattelijoiden hiljentämistä. Ei ole sattumaa, että DDR:ssä tarvittiin muuria ja Stasia hiljentämään dissidentit. Totuus on kuin maitohorsma – se kasvaa läpi betoninkin.

    Ideoiden tulee saada kilpailla vapaasti, se on välttämätöntä oikealle edistykselle. Sananvapauden välttämätön hinta on se, että joku aina pitää jotakin sopimattomana, mauttomana tai muutoin loukkaantuu. Sananvapaudelta ei voi kuitenkaan edellyttää sanojen järkevyyttä tai eleganssia, tyyliä.

    Ideoiden vapaa kilpailu näet vaatii laajasti tulkitun sananvapauden, sananvapausmyönteisen lainsäädännön ja oikeuskäytännön. Todistustaakan tulee olla aina sananvapauden rajoittajalla, ja tämän todistustaakan tulee olla ankara. Länsimaisen korkeakulttuurin ja todellisen liberalismin välimatka totalitaristiseen woke-valtioon on pelottavan lyhyt, ja se pyhitetään hiljaisuudella.